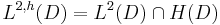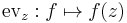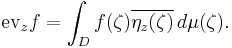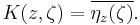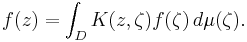Bergman kernel

In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cⁿ.

In detail, let L²(D) be the Hilbert space of square integrable functions on D, and let L^2,h(D) denote the subspace consisting of holomorphic functions in D: that is,

$L^{2,h}(D) = L^2(D)\cap H(D)$

where H(D) is the space of holomorphic functions in D. Then L^2,h(D) is a Hilbert space: it is a closed linear subspace of L²(D), and therefore complete in its own right. This follows from the fundamental estimate, that for a holomorphic square-integrable function ƒ in D

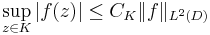
$\sup_{z\in K} |f(z)| \le C_K\|f\|_{L^2(D)}$

(1)

for every compact subset K of D. Thus convergence of a sequence of holomorphic functions in L²(D) implies also compact convergence, and so the limit function is also holomorphic.

Another consequence of (1) is that, for each z ∈ D, the evaluation

$\operatorname{ev}_z�: f\mapsto f(z)$

is a continuous linear functional on L^2,h(D). By the Riesz representation theorem, this functional can be represented as the inner product with an element of L^2,h(D), which is to say that

$\operatorname{ev}_z f = \int_D f(\zeta)\overline{\eta_z(\zeta)}\,d\mu(\zeta).$

The Bergman kernel K is defined by

$K(z,\zeta) = \overline{\eta_z(\zeta)}.$

The kernel K(z,ζ) holomorphic in z and antiholomorphic in ζ, and satisfies

$f(z) = \int_D K(z,\zeta)f(\zeta)\,d\mu(\zeta).$

References

Krantz, Steven G. (2002), Function Theory of Several Complex Variables, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2724-6 .
Chirka, E.M. (2001), "Bergman kernel function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b015560 .

Bergman kernel

See also

References